Mamma ho perso la password
 sottotitolo: che belle che sono le Rainbow Table
sottotitolo: che belle che sono le Rainbow Table
Nella mia esperienza mi son fatto convinto che la cartina al tornasole per stabilire se qualcuno passa troppo tempo davanti ad un computer è chiedere se ha mai dimenticato una password. Se la risposta è affermativa, si ha a che fare con un geek (nel mio caso ho dimenticato più volte una password!).
Mentre cazzeggiavo mi informavo sul web, mi sono imbattuto in ophcrack, un programma per crackare le password di Windows; tale programma fa uso delle cosidette Rainbow Table (d'ora in poi semplicemente RT). Il programma così com'è funziona anche per Vista, ma ha in generale alcune limitazioni: le RT incluse permettono di crackare solo password contenenti caratteri alfanumerici. Una password considerata "forte" non può essere perció crackata con la dotazione di RT del programma.
Una cosa carina è una versione LiveCD basata su Linux che una volta lanciata fa tutto da sola: carica le tabelle in memoria, individua il SAM, e in pochi minuti esegue la ricerca (10 minuti in tutto sulla mia macchina virtuale). Anche tale versione ovviamente è limitata alle password alfanumeriche. RT più complete sono in vendita un po' in giro (quella completa per coprire le password di Windows richiede 60GB di spazio su disco) ed i link sono disponibili nella pagina di ophcrack. Faccio notare che per poter crackare le password di Windows bisogna essere amministratori oppure avere accesso fisico al PC per fare il boot da CD (nel caso qualcuno voglia farsi tentare da aprire un baco).
Ma come funzionano le RT? Il meccanismo è un po' complicato e parafrasando Einstein ora che l'ho capito potrei anche spiegarlo agli altri. Nella spiegazione faccio riferimento ad un algoritmo "semplificato".
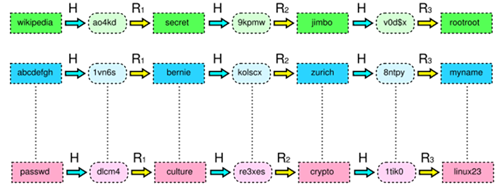
Le password vengono di solito memorizzate usando una funzione hash che data una password restituisce una stringa "complicata" (d'ora in poi semplicemente hashcode). La funzione hash non è invertibile nel senso che è impossibile trovare una semplice funzione matematica che dato un hashcode restituisca la password. Per generare le RT, viene definita una funzione reduce che dato un hashcode restuisca una nuova password (diversa da quella che ha generato l'hashcode: in parole povere la funzione reduce non è l'inversa della funzione hash in quanto l'inversa come già detto non esiste). Di tale nuova password viene generato un nuovo hashcode il quale verrà poi dato in pasto alla funzione reduce che genererà una nuova password, ecc. ecc. Il tutto per un discreto numero di volte (nell'esempio qui sotto riportato da WikiPedia l'operazione viene effettuata tre volte). In realtà in ci sono diverse funzioni reduce, una per ogni passaggio (nella figura indicate come R1, R2, R3)
Nell'esempio sopra si parte da password a caso (wikipedia, abcdefgh, passwd) si calcola l'hashcode corrispondente (ao4kd, 1vn6s, dicm4); poi si applica la prima funzione reduce (R1) e si ottiene una nuova password (secret, bernie, culture) e si ripete con le successive funzioni fino ad ottenere l'ultima password (rootroot, myname, linux23). Alla fine di questi semplici passaggi si memorizza nella RT solamente la password di partenza e quella di arrivo.
Nel caso di cui sopra si avrà una RT fatta in questa maniera:
| wikipedia | rootroot |
| abcdefgh | myname |
| passwd | linux23 |
E ora arriviamo al dunque: come si calcola la password dato un hashcode e una RT? In questo modo:
- prendere l'hashcode in ingresso e applicare l'ultima funzione reduce ottenendo una nuova password
- confronta tale password con una delle password contenute nella colonna di destra della RT
- se la password non esiste nella colonna di destra, applicare all'hashcode di partenza la penultima funzione reduce ottenendo una nuova password, calcolarne l'hashcode e usarlo come nuovo hashcode tornando al punto 1.
- se la password invece esiste, restituire al chiamante il valore corrispondente sulla colonna sinistra.
Ora se la RT è completa e l'hashcode iniziale è valido, alla fine del loop si avrà una password di partenza da dare in pasto ad un'altra funzione che prende in ingresso l'hashcode di partenza e la password trovata dalla procedura precedente, seguendo iterativamente i seguenti passi:
- calcolare l'hashcode della password
- se coincide con l'hashcode di partenza la password cercata è quella
- se non coincide con l'hashcode di partenza genera una password usando la funzione reduce e ricomincia da 1.
Un esempio: sia secret la password da cercare. Secondo la figura, il suo hashcode è 9kpmw; quindi l'obiettivo sarà trovare la password associata a 9kpmw.
Applicando la prima procedura con la funzione R3 otteniamo come prima nuova password pippo. pippo non è nella tabella (colonna a destra) e quindi si itera ancora. Si applica la R2 all'hashcode di partenza ottenendo jimbo, quindi si calcola l'hashcode di jimbo che stando alla figura è v0d$x e da questo generiamo una nuova password usando stavolta R3(rootroot). In questo caso la procedura si ferma perché rootroot è presente nella RT ed è associata a wikipedia come password di partenza.
Ora tocca avviare la seconda procedura usando wikipedia e 9kpmw.
Si calcola l'hashcode di wikipedia ottenendo ao4kd. Siccome non è l'hashcode che si sta cercando, si fa un'altra iterazione. ao4kd usando la funzione reduce genera secret. Si calcola l'hashcode di secret che è 9kpmw: ovvero l'hashcode di partenza. La password cercata quindi è secret.
Con l'algoritmo vero ogni entry della tabella è generato attraverso svariate iterazioni (nell'ordine di diverse migliaia). E a complicare le cose nella realtà può accadere che la prima procedura procuri un falso positivo nel qual caso bisogna continuare ad iterare: dato un buon insieme di funzioni reduce, per generare le RT che coprono tutte le possibili password di Windows sono richiesti diversi anni calcolo. Le RT oggi disponibili sono state infatti ottenute attraverso sistemi di network computing.
La bellezza di questa tecnica è la totale indipendenza dalla funzione di hash. Quindi si può applicare per generare RT anche per altri algoritmi (MD5 ad esempio). Resta infine da dire che per invalidare l'uso delle RT basta un semplice algoritmo di salting. Tanto di cappello all'inventore di tale tecnica, Philippe Oechslin.
-enjoy